Flow Dynamics – Chapter 10

Understand the concept of Work in the RLFlow Model.

Work in RLFlow

Redefining the Classical Understanding of Work

In classical physics, the concept of work was initially laid out by pioneers like Isaac Newton and James Clerk Maxwell. They provided us with an understanding of work as the product of force and displacement, encapsulated in the equation:

W = F · d

• F: The force applied.
• d: The distance over which the force acts.

This equation measures how much energy is used to move an object through space. Simple, yet effective.

In the RLFlow model, however, we look at the universe as a network of flows rather than separate objects being “pushed” by forces. Here, work isn’t about applying force on a static mass; rather, it arises when flows interact, reshaping each other’s velocity and resonance.

Work as Flow Interaction:
At its core, work in RLFlow describes how two (or more) flowfields converge or diverge, exchanging energy and reorganizing themselves. Instead of focusing on a single push or pull, we ask: How do flows meet, adjust their intensities, and change velocity?

Mathematical Representation:

W_flow(x, t) = ∫(R₁(x, t) · R₂(x, t)) · Δv_flow dx

• R₁(x, t) and R₂(x, t): The resonance intensities of the interacting flows, reflecting their density, stability, and strength.
• Δv_flow: The change in flow velocity resulting from their meeting—analogous to displacement in classical work.

This equation states that work is the energy exchanged when flows merge or diverge, altering velocity and resonance. One flow can gain energy while another loses it—much like two rivers colliding may generate new eddies or a calm merge, depending on how intensities combine.

Here’s how energy transformations unfold:

• Resonance Energy reflects the stability of each flow before interaction. Stronger resonances drive the flow’s ability to influence its counterpart.
• Kinetic Energy emerges as velocity changes ripple across the system, creating motion or turbulence.
• Potential Energy forms when reconfigurations store energy in newly stabilized or constrained flow patterns.

Ultimately, work in RLFlow means reshaping the flowfield itself—shifting velocities, building or breaking resonances—to create new configurations of energy in motion.

The RLFlow Work Equation and Energy Transfer

In RLFlow, work reflects how flows reorganize energy within the flowfield—a notion that diverges sharply from classical mechanics:

• Classical Mechanics: Work measures how a static force pushes an object from point A to point B.
• RLFlow: Work is the dynamic interplay between flows, where energy is redistributed not only to generate motion but also to reshape velocity and resonance throughout the system.

This approach highlights a more fluid and interconnected understanding of how energy moves in the universe. Instead of picturing force acting on discrete masses, RLFlow emphasizes continuous motion everywhere. “Work” emerges from harmonizing those motions, rather than forcing one object to move under another’s influence.

Consider a person pushing a box in classical terms. In RLFlow, the “person” and the “box” are two flow systems that merge and interact. The resulting work doesn’t just relocate the box; it reshapes how the flows themselves combine—altering resonance, velocity, and overall stability for both parties.

Thus, RLFlow broadens the concept of work beyond mere displacement. It’s about modifying the flowfields—changing speed, direction, and the way energy is configured—so that the final arrangement balances all interacting flows in a new pattern of motion. This emphasis on fluidity and connection underscores RLFlow’s shift away from a world of isolated forces toward a universe of ever-evolving, interwoven streams of energy.

Work as Reshaping Flowfields:

In RLFlow, work goes beyond applying force to move an object. It’s about how entire flowfields transform when they come into contact, making energy exchange more dynamic than in classical mechanics. Suppose two distinct flows merge; each has its own resonance and velocity. Their interaction shifts these characteristics—that shift is what RLFlow calls work.

Consider two streams converging into a single river. At their junction, you’ll see whirlpools, eddies, and brand-new currents forming. That meeting point exemplifies RLFlow work: it’s not just water in motion, but a deeper reconfiguration of velocities and resonance patterns within the flow. New currents emerge, old flows merge or dissipate, and energy redistributes throughout.

Mathematical Representation:

W_flow(x, t) = ∫(R₁(x, t) · R₂(x, t)) · Δv_flow dx

• R₁(x, t) and R₂(x, t): Denote the resonance intensities of the interacting flows, indicating their stability and strength.
• Δv_flow: Tracks how each flow’s velocity changes upon interaction.

In other words, we shift from the classical notion of forces pushing objects to a perspective of flows reshaping one another through energy exchange. Work in RLFlow is about altering how energy is arranged—flows with higher intensity exert greater influence, and any velocity adjustment reflects the work accomplished by that influence.

Metaphor to Explain Work in RLFlow

Think of two streams flowing into a single river. Each has its own resonance—a combination of intensity and stability. When these streams meet, new patterns emerge: whirlpools, eddies, or straight currents. This merging isn’t just water changing direction; it’s energy being redistributed, altering velocity and resonance in both flows.

The Work here is the reconfiguration that unifies them into one current—shifting speeds, directions, and overall structure. A stronger stream naturally exerts greater influence on a weaker one, “doing more work” to reshape the combined flowfield. In RLFlow, then, work isn’t about an external force on an object; it’s the dynamic interplay among flows that transforms how energy is arranged.

Visualize standing by a river where a powerful current merges with a gentler one. You’d see turbulence, new eddies, and eventually a single, merged flow. That’s RLFlow work in action—energy transfers and resonates, creating stable or dynamic patterns as flows adapt to each other.

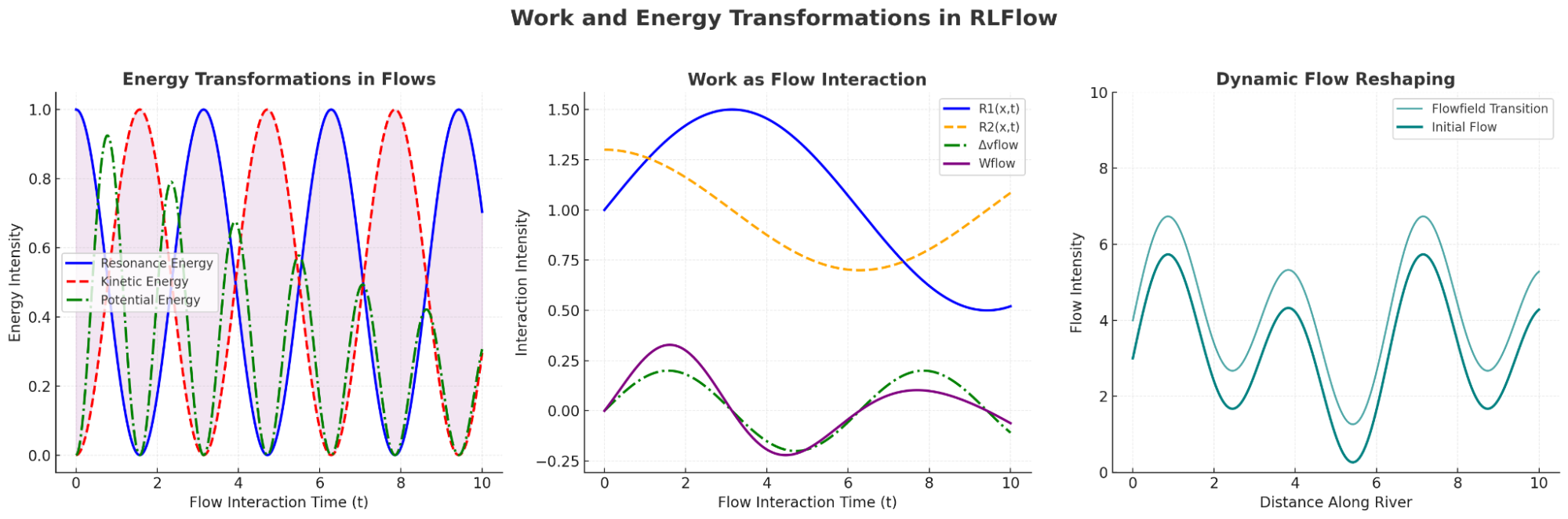
Energy Transformations in Flows

Shows the relationship and transitions between resonance, kinetic, and potential energy over time:
In RLFlow, energy transitions are fluid and dynamic, moving between resonance (stable energy patterns), kinetic (motion energy), and potential (stored energy) forms. These transformations occur seamlessly, demonstrating the adaptability of the Flowfield to external influences and internal adjustments.

Work as Flow Interaction

Demonstrates the RLFlow work equation:

W_flow(x, t) = ∫(R₁(x, t) · R₂(x, t)) · Δv_flow dx

• R₁(x, t): The resonance intensity of one flow, indicating its density and stability.
• R₂(x, t): The resonance intensity of another flow, reflecting its strength and organization.
• Δv_flow: The change in velocity as the flows interact.

This equation captures how the interaction of two flowfields produces work by redistributing energy, reshaping velocities, and altering resonance patterns. It highlights how energy exchange and transformation are fundamental to RLFlow's concept of work.

Dynamic Flow Reshaping (River Metaphor)

Visualizes the merging and transformation of flows as streams converge:
Imagine two streams merging into a single river. At the convergence, the interaction creates whirlpools, eddies, and new currents—illustrating the redistribution of energy. The river metaphor explains how flows adjust their resonance and velocity, transforming energy into new configurations.

Key Points of the River Metaphor:

• Whirlpools represent localized increases in resonance intensity.
• New currents reflect the redistribution of kinetic energy.
• Eddies show areas where potential energy stabilizes into resonance patterns.

This metaphor demonstrates how RLFlow captures the dynamic nature of flows, where energy is never lost but constantly transformed and redistributed across the Flowfield.

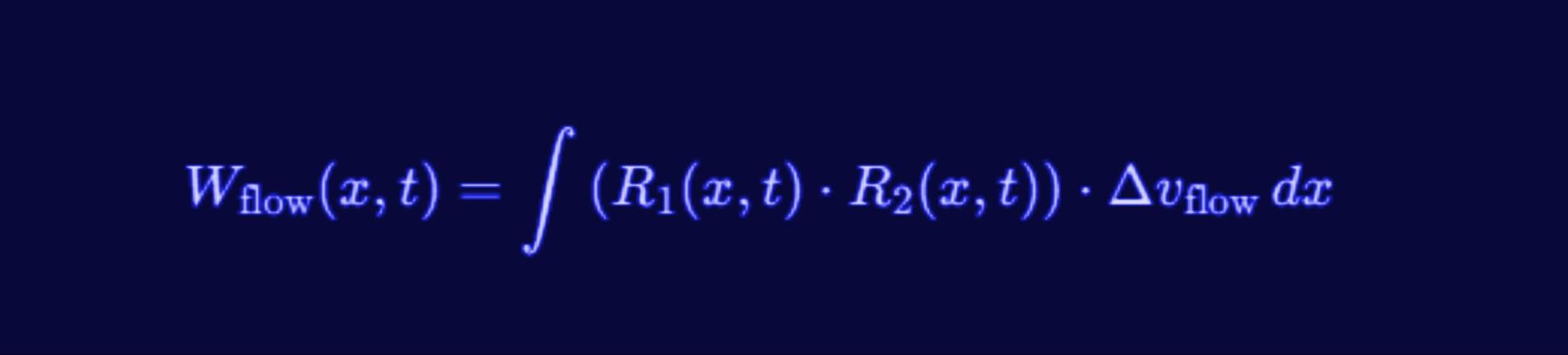
W_flow(x, t): Work Done by Interacting Flows

• Represents the work done by interacting flows over a spatial region.
• In RLFlow, work is not just force applied over a distance but a measure of the energy exchanged between two interacting flow structures.

R₁(x, t) and R₂(x, t): Resonance Intensities of Interacting Flows

• These are the resonance intensities of the interacting flows at position x and time t.
• They describe the stability, coherence, and strength of each flow’s resonance.
• Higher resonance intensity means a more coherent and impactful flow interaction.

Δv_flow: Change in Flow Velocity

• Represents the change in flow velocity as a result of the interaction.
• Tracks how the momentum and speed of the flow structures adjust when interacting.
• Analogous to how forces cause velocity changes in classical physics, but in RLFlow, this results from the redistribution of flow resonance.

∫ dx: Integration Across the Flowfield

• The integral sums up the contributions of all infinitesimal flow interactions over the spatial region of interest.
• This accounts for the cumulative effect of flow resonance changes across space.

Interpretation in RLFlow

• Flow Work is the process by which one flow structure influences another, transferring energy through resonance interactions.
• Unlike classical work, which depends on force and displacement, RLFlow work emerges from the interplay of flow intensities and velocity shifts.
• This equation provides insight into how flows exchange energy, self-organize, and maintain stability across scales.

Summary of RLFlow Work

Ultimately, work is the energy exchange that arises when flows interact and reorganize. It’s not merely pushing something over a distance but reshaping how flows link together. Resonance intensities decide how strongly each flow can “push back,” and the resulting velocity changes track where the energy goes. Everything is in motion, and work is about continually evolving these flow relationships—a far richer, more interconnected perspective than the classical model of force times displacement.