Flow Dynamics – Chapter 11

Explore the conservation of Angular Momentum in the RLFlow Model.

Conservation of Angular Momentum

Angular Momentum: From Classical Physics to Flow Dynamics

Classical Physics:
Angular momentum, a cornerstone of physics, is the rotational counterpart to linear momentum. Classical physics describes angular momentum as the product of an object’s mass, velocity, and its distance from a rotational axis, captured by the equation:

L = r × p = m · (r × v)

• L: Angular momentum.
• r: Position vector relative to the axis of rotation.
• p: Linear momentum.
• m: Mass of the object.
• v: Velocity of the mass.

Classically, angular momentum is conserved in the absence of external torque. This principle explains phenomena like planetary orbits, gyroscopic stability, and the acceleration of a figure skater pulling in their arms. However, these phenomena are traditionally framed as discrete objects with isolated momentum, ignoring the interconnected nature of the universe.

RLFlow Reimagines Angular Momentum

In the RLFlow model, angular momentum emerges not as an isolated property of objects but as a manifestation of rotational stability within the universal Flowfield. Flows, not static objects, dominate the RLFlow perspective. Rotational persistence arises from the stability of resonant flows interacting dynamically within the interconnected Flowfield.

Key Shift:
Classical View: Angular momentum is an isolated property tied to mass and motion.
RLFlow View: Angular momentum emerges from the stability of rotational flows within the Flowfield, governed by resonance and energy transformations.

Flow-Based Angular Momentum Equation

In RLFlow, angular momentum is described by the resonance intensity and rotational flow potential across the Flowfield:

L_flow(x, t) = ∫₀^∞ R(x, t) · Φ_rot(x, t) dx

• L_flow(x, t): Angular momentum in the Flowfield.
• R(x, t): Resonance intensity, representing flow density and stability.
• Φ_rot(x, t): Rotational flow potential, describing the rotational configuration of flows at point x and time t.

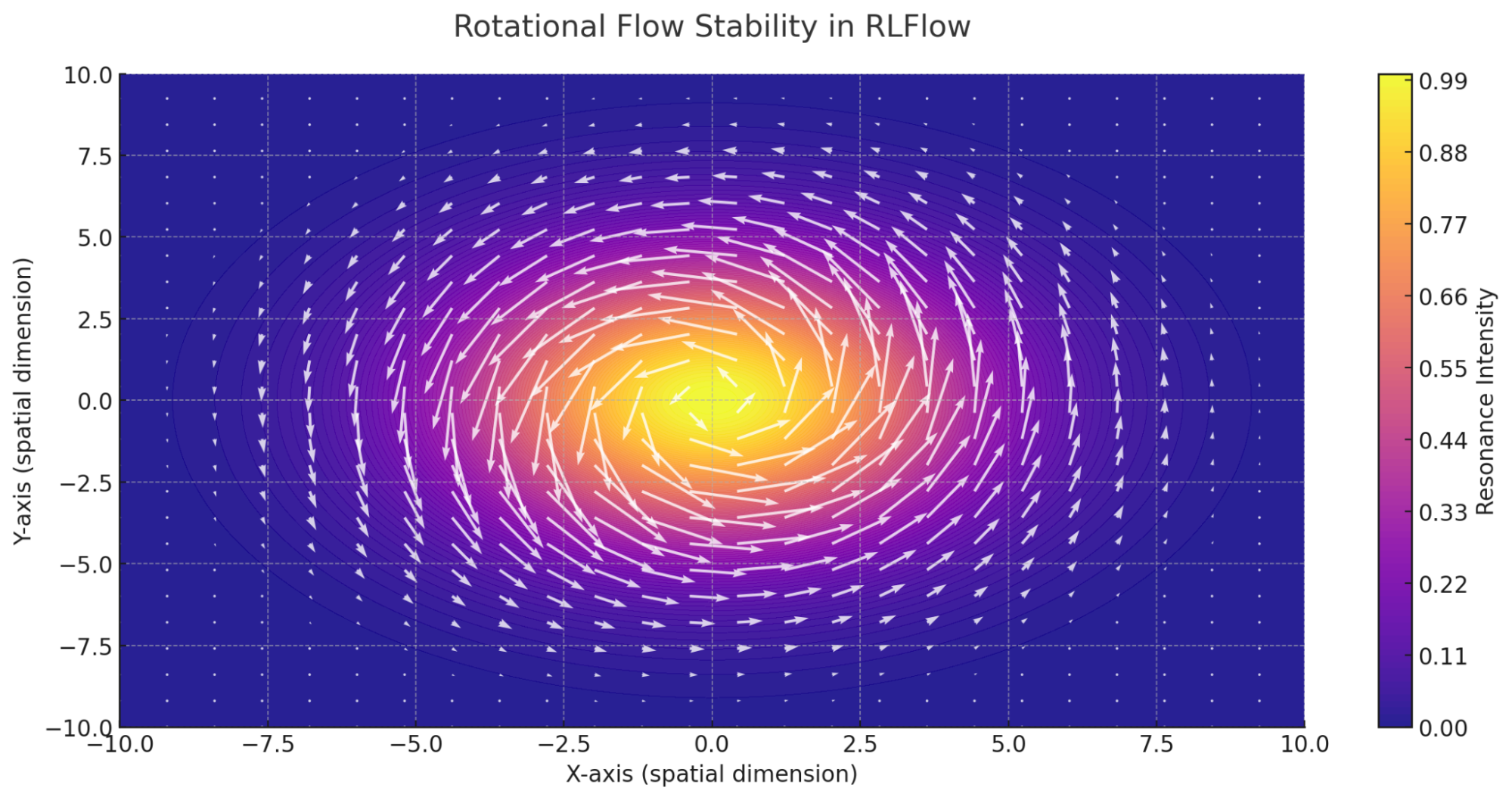
This visualization illustrates how stable rotational flows emerge in RLFlow, showing how resonance intensity maintains angular momentum. The vector field represents rotational motion, while the color gradient highlights resonance stability, reinforcing RLFlow’s view of angular momentum as a persistent, dynamic property of the flowfield.

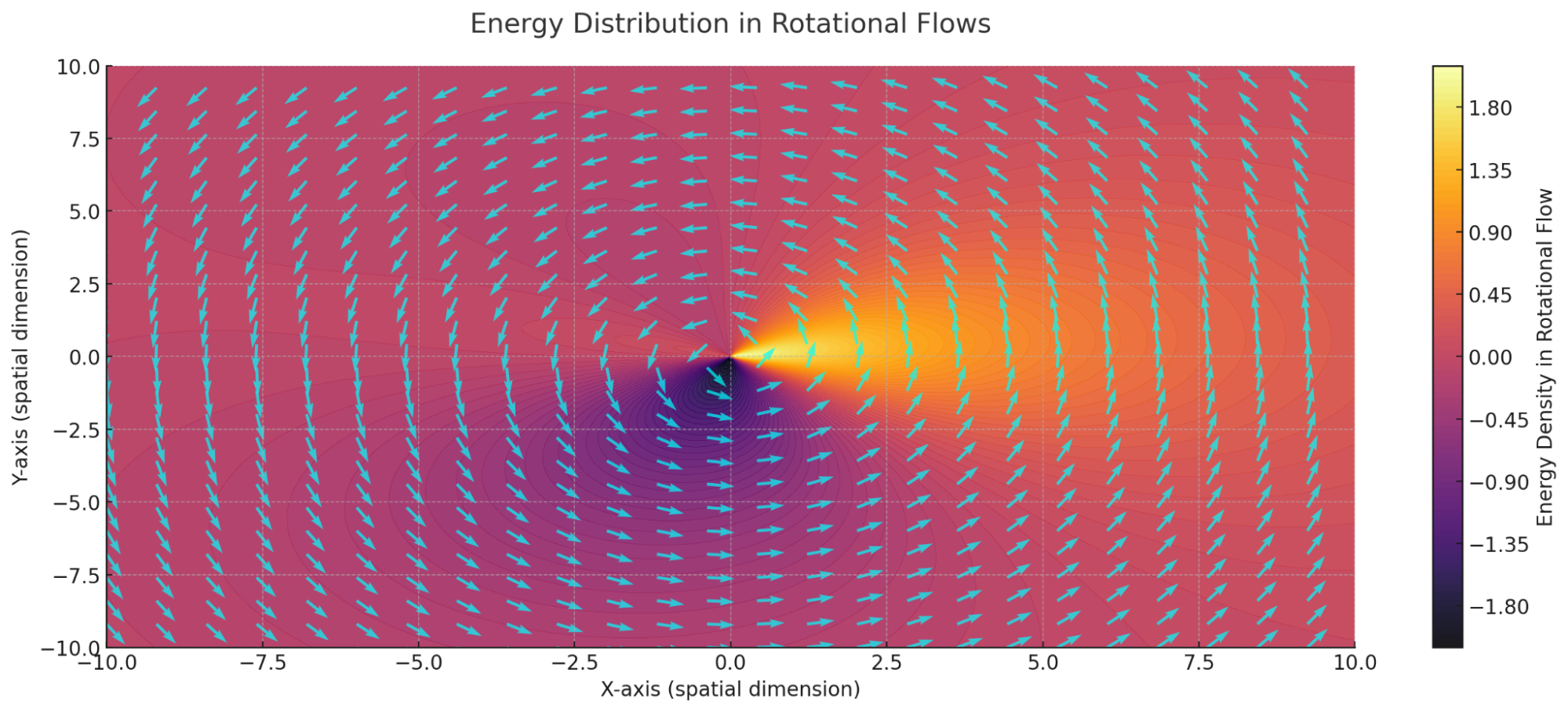
Energy Distribution in Rotational Flows within RLFlow. The color-coded heatmap represents how energy transforms between resonance, kinetic, and potential forms across a rotating system.

• Bright regions indicate high energy density, where flows are most concentrated.
• Cooler regions show areas where energy has dissipated or stored as potential.
• Cyan velocity vectors overlay the heatmap, depicting the motion of energy through the system, revealing the continuous redistribution of flow intensities.

Interpretation:
Angular momentum in RLFlow is the cumulative stability of rotational flows, not a property of individual objects. Resonance intensity reflects the flow’s ability to maintain rotation, while rotational potential describes the configuration of rotational motion.

Metaphor: Rotational Flow Stability

Imagine a whirlpool in a river. The swirling water represents a rotational flow pattern, maintained by the stability of its resonance. In RLFlow, angular momentum is the persistence of that resonance—a dynamic balance within the Flowfield that keeps the whirlpool spinning until disrupted by external forces.

• Classical View: Focuses on the water’s mass and velocity.
• RLFlow View: Emphasizes the stability and resonance of the flow creating the whirlpool.

Connecting Angular Momentum to the RLFlow Triad of Energies

Angular momentum is deeply tied to the three primary forms of energy in RLFlow:

• Resonance Energy: Stability of rotational flows (R(x, t)).
• Kinetic Energy: Motion within the rotational Flowfield.
• Potential Energy: Stored energy in the rotational configuration (Φ_rot(x, t)).

The conservation of angular momentum reflects the interplay of these energies, maintaining stability across the Flowfield.

Angular Momentum in RLFlow: From Quantum Spin to Galactic Rotations

Microscopic Systems: Angular Momentum in the Quantum Realm

• Classical Physics: Angular momentum depends on mass, velocity, and position. However, in quantum mechanics, angular momentum (or spin) is an intrinsic property of particles, seemingly independent of physical rotation.
• RLFlow Perspective: Spin is reimagined as the rotational resonance of quantum flow vortices. Particles are localized flow patterns where intrinsic angular momentum reflects the stability of these resonances.
• Pauli Exclusion Principle: RLFlow explains this principle as resulting from incompatible rotational resonances. Certain flow configurations cannot coexist without disrupting stability, reflecting why no two fermions can occupy the same quantum state.
• Quantum Angular Momentum Conservation:

• Example: Quantum Entanglement: Two entangled particles share a common resonance. When one particle’s flow state changes, the other’s resonance adjusts to conserve the overall rotational stability, maintaining angular momentum across the system.

Macroscopic Systems: Stability of Celestial Rotations

• Celestial Orbits as Flow Stability: Planets and stars are nodes within a resonant flowfield. Angular momentum emerges from the stability of rotational flows around massive bodies, maintained by resonance.
• Example: Planetary Orbits: A planet’s angular momentum results from the resonance between its orbital flow and the flowfield surrounding its star, ensuring predictable motion over time.
• Spiral Galaxies: The rotation curves of spiral galaxies—where outer stars move faster than predicted—are explained by RLFlow as the result of hidden flows and resonances within the galactic flowfield, conserving angular momentum without invoking additional matter.

Torque: Changing Rotational Resonance

In classical mechanics, torque is the force that changes an object’s angular momentum. In RLFlow, torque is redefined as the interaction of flows that disrupt or enhance rotational stability, altering the resonance of the flowfield.

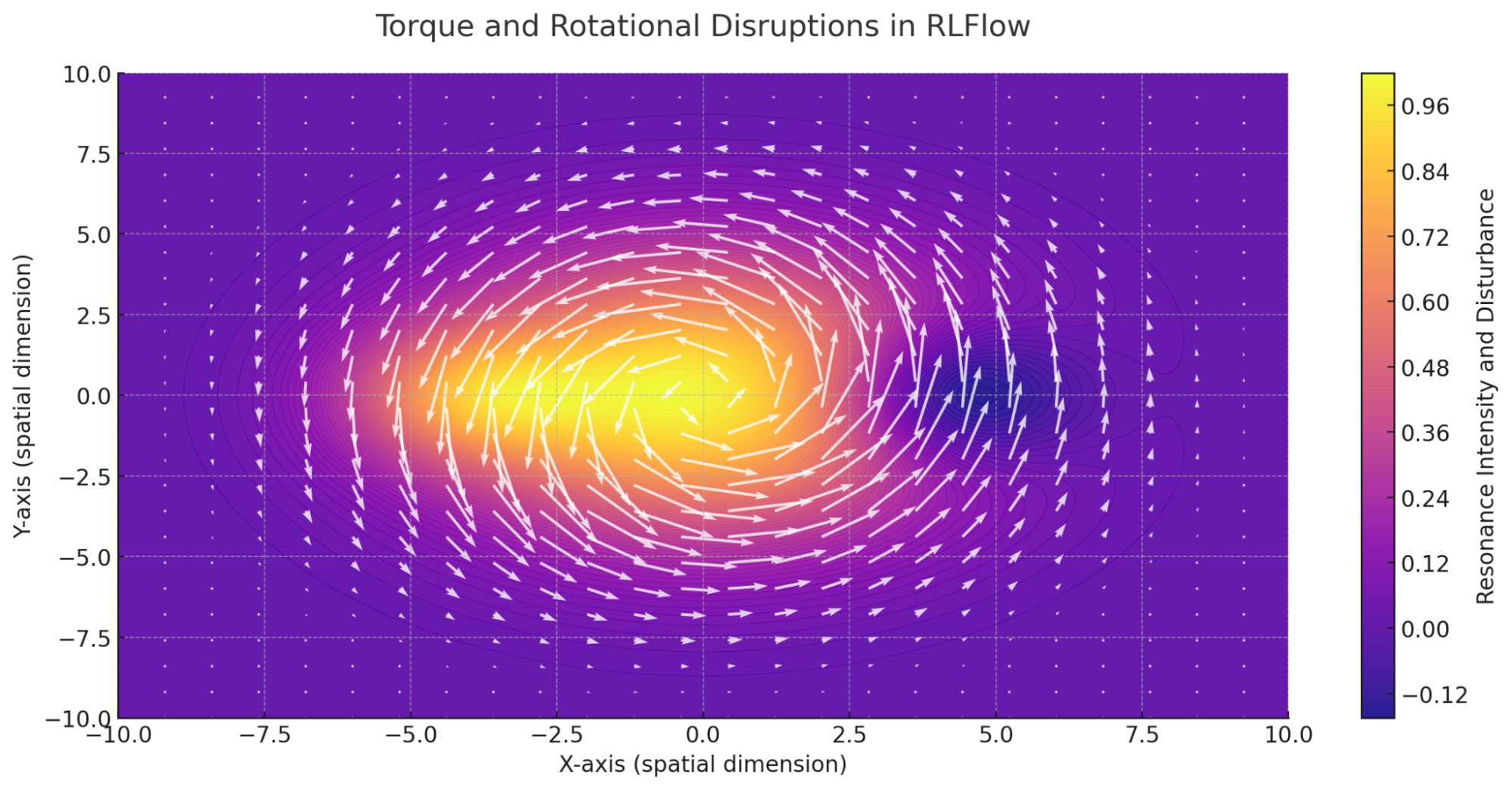
Torque and Rotational Disruptions in RLFlow:
This visualization illustrates how an external force (torque) disrupts a stable rotational flow in RLFlow. The color map represents resonance intensity, while the overlaid vectors show the swirling motion of the flow. External disturbances alter the vortex stability, shifting rotational resonance and influencing the surrounding flow dynamics.

RLFlow Torque Equation:

τ_flow(x, t) = ∫ R₁(x, t) · R₂(x, t) · ΔΦ_rot(x, t) dx

• τ_flow(x, t): Flow torque, representing changes in rotational stability.
• R₁(x, t) and R₂(x, t): Resonance intensities of interacting flows.
• ΔΦ_rot(x, t): Change in rotational flow potential.

Metaphor: Nudging a Spinning Top
Torque in RLFlow is like nudging a spinning top. The top represents a stable rotational flow, and the nudge is an external flow interaction. This alters the top’s rotational resonance, causing it to wobble, speed up, or slow down. The flowfield adjusts dynamically to preserve overall angular momentum.

Implications for Large-Scale Structures

• Gravitational Waves: The rotational resonance of massive binary systems creates ripples in the flowfield, conserving angular momentum while redistributing rotational energy as gravitational waves.
• Black Hole Spin: A black hole’s angular momentum reflects the concentrated rotational resonance of its surrounding flows. RLFlow suggests this spin is a dynamic interaction with the surrounding flowfield, not just an internal property.

Universal Conservation of Angular Momentum

In RLFlow, the conservation of angular momentum is not limited to discrete systems like planets or particles; it reflects a universal principle of flow conservation. Angular momentum emerges from the stability of rotational flows, maintaining balance across the entire Flowfield, from subatomic particles to galactic superstructures.

Conservation Across Scales

• Rotational Symmetry: In classical physics, conservation laws are tied to symmetries, as demonstrated by Emmy Noether’s theorem. In RLFlow, rotational symmetry in the Flowfield ensures that angular momentum is conserved as flows adapt to disturbances.
• Dynamic Redistribution: When rotational flows are disrupted, the Flowfield redistributes resonance and velocity to preserve the total angular momentum. This principle applies equally to quantum systems and cosmic phenomena, reinforcing the interconnectedness of the universe.

Applications of Angular Momentum in RLFlow

1. Stabilizing Hurricanes and Atmospheric Flows

• RLFlow Perspective: A hurricane’s angular momentum is the result of coherent rotational flows that stabilize despite external influences like wind shear or land interaction.
• Practical Application: By understanding how rotational resonance maintains hurricanes, we could develop methods to disrupt these flows, potentially weakening storms before landfall.

2. Quantum State Manipulation

• RLFlow Perspective: Manipulating the resonance of quantum flows allows precise control of angular momentum, enabling advancements in quantum computing through enhanced qubit stability.
• Practical Application: By tuning the resonance of quantum flows, we could extend the coherence time of qubits, improving computational efficiency and error correction.

3. Galactic Dynamics and Dark Matter

• RLFlow Perspective: Galaxies are stabilized by coherent flows that extend beyond visible matter, creating the rotational patterns observed without requiring exotic particles.
• Practical Application: Flow resonance mapping of galaxies could reveal the underlying flow structures, offering an alternative explanation for dark matter effects.

Broader Cosmological Implications

1. Formation of Cosmic Structures

• Cosmic Web: The interconnected filaments of the cosmic web are regions where rotational flows converge, creating stable configurations that persist over billions of years.
• Rotational Patterns: RLFlow suggests that the spiral structure of galaxies and the alignment of galaxy clusters are emergent patterns of rotational resonance.

2. Black Holes and Angular Momentum

• Energy Redistribution: As matter spirals into a black hole, the rotational resonance intensifies, concentrating angular momentum at the event horizon. This aligns with RLFlow’s principle of flow redistribution, where energy is neither created nor destroyed but dynamically reconfigured.

RLFlow’s Broader Conservation Principles

• Energy Transformation: Rotational flows convert kinetic energy into potential energy and vice versa, maintaining the total flow intensity.
• Momentum Interactions: Linear and angular momentum are seamlessly connected in RLFlow, with rotational flows influencing linear trajectories through resonance coupling.
• Stability Across Scales: The conservation principles in RLFlow apply universally, ensuring coherence from quantum spins to cosmic rotations.

Practical and Philosophical Insights

Practical Applications

• Weather Prediction: Understanding rotational flow stability could improve models for hurricanes, tornadoes, and atmospheric currents.
• Energy Efficiency: Devices like turbines and rotors could be optimized using RLFlow principles to harness rotational resonance more effectively.
• Space Exploration: RLFlow could inform spacecraft design by leveraging flow resonance to maintain stability during rotation and thrust adjustments.

Philosophical Insights

• Interconnected Universe: RLFlow highlights the unity of all physical phenomena, showing that angular momentum is not an isolated property but a dynamic expression of universal flow interactions.
• Emergent Order: The conservation of angular momentum in RLFlow reflects the natural tendency of flows to organize into stable patterns, offering a deeper understanding of the universe’s inherent order.

Flow-Based Angular Momentum
This equation redefines angular momentum in RLFlow, illustrating how rotational stability emerges from the mutual influence of resonance intensity and rotational flow potential. Just as flows shape forces, they also weave the fabric of spin and motion in the dynamic Flowfield.

Flow-Based Angular Momentum in RLFlow: This equation expresses angular momentum as the cumulative effect of resonance stability and rotational potential across the flowfield, emphasizing the continuous and interconnected nature of rotational motion in RLFlow.

Conclusion

RLFlow’s reinterpretation of angular momentum transforms our understanding of rotational stability across scales. By framing angular momentum as an emergent property of flow resonance, RLFlow connects phenomena as diverse as quantum spin, planetary orbits, and galactic rotations under a single, unified framework.

In this vision, angular momentum is no longer confined to discrete masses or classical mechanics. It is a dynamic, universal property of flows—woven into the fabric of the universe and conserved through the endless dance of resonance and adaptation. This broader perspective invites new applications, from quantum technologies to cosmological discoveries, showcasing the power of RLFlow as a unifying principle of physics.