Flow Dynamics – Chapter 9

Explore the principle of Conservation of Flow Intensity in the RLFlow Model.

Conservation of Flow Intensity in RLFlow

Introduction: Classical Conservation of Energy

In classical physics, the principle of conservation of energy stands as one of its most fundamental ideas. It holds that energy can neither be created nor destroyed, only transformed—whether it’s potential energy turning into kinetic or electrical energy becoming thermal. Across countless processes, the total amount of energy in an isolated system remains unchanged.

From Isaac Newton to James Clerk Maxwell, scientists have used this principle to explain phenomena from planetary orbits to electromagnetic waves. In that traditional view, energy is often treated as a discrete quantity residing in individual systems or objects, passed from place to place like a commodity.

But what if energy isn’t merely “stored” in objects? RLFlow suggests a different perspective: energy is an aspect of the flowfield, a constantly evolving property of interconnected flows. Instead of picturing energy as static chunks that move between isolated bodies, RLFlow sees it as flow intensity woven throughout the universe.

Conservation of Flow Intensity

In RLFlow, conservation of energy is better framed as conservation of flow intensity. This subtle shift moves away from the notion of energy as a stockpile owned by particular particles, and instead emphasizes resonance and dynamic adaptation across the entire flowfield.

Flow Intensity Conservation Explained

• Dynamic Quality
  Energy in RLFlow is not a tally of how many “energy units” exist; it’s a continuously reshaping characteristic of the flow. Think of it less like a coin purse you guard and more like a current in a river—always adjusting its depth, speed, and direction while the overall “volume” remains intact.
• Adaptation, Not Storage
  When two flow structures meet—like a whirlpool colliding with a wave—energy isn’t simply tossed from one to the other. Instead, flow intensity is redistributed. The system rebalances itself to preserve the total intensity, somewhat like how dancers in a troupe keep the overall routine seamless even if their individual steps shift.

In other words, RLFlow’s principle of conservation doesn’t revolve around preserving lumps of energy, but around maintaining the consistent intensity of the flow throughout its ongoing transformations.

A Three-Part View of Energy in RLFlow:
Having identified three primary forms—Resonance, Kinetic, and Potential—RLFlow captures total energy with a more explicit formula:

E_total(x, t) = ∫(R_resonance(x, t) + R_kinetic(x, t) + R_potential(x, t)) dx

• R_resonance(x, t): The “rest-like” energy that comes from stable flow patterns.
• R_kinetic(x, t): The moving, dynamic energy reflecting flow velocity and momentum.
• R_potential(x, t): The stored capacity for future change in a flow’s configuration.

No matter how these individual components vary, the integral representing the system’s total flow intensity remains constant—fulfilling RLFlow’s broader conservation principle.

Dynamic Transformations in RLFlow:
Within this framework, the total E_total doesn’t fluctuate, but the form of energy can change from one type to another. A few classic transitions:

• From Potential to Kinetic:
  Think of water behind a dam—traditionally called “potential energy.” When released, that water surges forward, turning into motion (kinetic). In RLFlow terms, a previously stable configuration of flows (R_potential) transitions into a dynamic, moving flow (R_kinetic). The total flow intensity doesn’t vanish or appear anew; it merely rearranges.
• From Kinetic to Resonance:
  Consider a fast-moving current that stabilizes into a gentle whirlpool. What was once vigorous motion is partially converted into a stable flow pattern (R_resonance). Instead of “losing energy,” the system refocuses it into a calm but coherent state.
• From Resonance to Potential:
  Sometimes a stable whirlpool or calm section of flow can reorganize into a heightened arrangement—like water piling up behind a partial barrier, quietly building capacity (R_potential). That “rest-like” resonance has evolved into a stored form of energy ready to unleash motion if the barrier is breached.

In every shift, the combined total of R_resonance + R_kinetic + R_potential remains invariant. RLFlow’s conservation principle ensures that energy cannot “disappear” or be “created” but is instead restructured within the flowfield.

Why This Matters

1. A More Fluid Perspective
Traditional physics sees energy as something contained in objects or fields. RLFlow says it’s an aspect of the entire flow, with each region’s intensity constantly shaped by interactions. Conservation thus becomes holistic, spotlighting the entire network rather than isolated exchanges.

2. Emphasis on Adaptation
Where classical views stress “energy transfer,” RLFlow focuses on rebalancing. The “flow intensity” is never lost—only refashioned among its resonance, kinetic, and potential states.

3. Connecting Scales
From a trickle of water to vast cosmic flows, RLFlow’s conservation principle applies at all levels. Whether describing micro-quantum fluctuations or massive astrophysical jets, the same idea persists: total flow intensity is safe from annihilation or genesis, perpetually conserved as it metamorphoses among forms.

In RLFlow, conservation of energy is best understood as conservation of flow intensity. Where classical physics sees distinct “buckets” of energy transferred between objects, RLFlow envisions a continuum of resonance, kinetic, and potential energies seamlessly shifting within an interconnected flow. The net intensity in any closed system never wavers; it only finds new expressions as flows merge, diverge, or transform.

This perspective not only encapsulates classical ideas—like potential turning into kinetic—but also broadens them. It situates energy conservation in a universe where everything is in motion and everything is connected, and where the deep structure of reality is an ever-adapting fabric of flow.

Flow-Based Conservation Equation:
To capture the total energy in RLFlow mathematically, we unify resonance, kinetic, and potential energies under one integral. Rather than describing separate, isolated energy chunks, this approach shows how all forms of flow resonance contribute to a single conserved quantity:

E_total(x, t) = ∫(R_resonance(x, t) + R_kinetic(x, t) + R_potential(x, t)) dx

Where:

• E_total(x, t):
  Represents the total energy at a given region of the flowfield, combining the different expressions of flow resonance at each point x and time t.
• R_resonance(x, t):
  The intrinsic or “rest-like” energy arising from stable flow patterns.
  (Related to the “First RLFlow Law”—Flow Stability.)
• R_kinetic(x, t):
  The energy tied to motion within the flow—the portion arising from the velocity and momentum-like properties of flowing systems.
  (Related to the “Second RLFlow Law”—Flow Interaction.)
• R_potential(x, t):
  The stored or “configurational” energy reflecting how flows are arranged with capacity to shift or do work.
  (Related to the “Third RLFlow Law”—Reciprocal Flow.)

This equation shows how three distinct forms—resonance, kinetic, and potential—sum to provide the system’s total flow intensity. According to RLFlow, energy conservation means that while these components can transform (for example, potential converting to kinetic), the overall integral of resonance across the flowfield remains constant.

Flow patterns may reorganize or redistribute energy among resonance, kinetic, and potential states, but the total flow intensity never vanishes or spontaneously appears.

Metaphors to Illustrate Flow Intensity Conservation

The River of Flow

Picture a wide, continuously moving river. Some parts rush swiftly, teeming with kinetic energy (the flow’s motion), while other areas form calmer pools—like potential reservoirs waiting to be unleashed. The deeper or more tranquil a pool, the more “stored” energy it can hold, akin to RLFlow’s notion of a stable, resonant pattern.

When water spills over a waterfall, what was potential energy behind the drop transforms into kinetic energy as it plunges. In RLFlow, this is no simple handoff of energy “units”—it’s a shift in flow intensity. The total remains constant, yet the river reconfigures how it expresses that intensity, from stillness to rapid motion and back again.

The Dancing Flows

Now picture dancers in a grand ballroom, each representing a flow structure. Sometimes they spin quickly (kinetic), sometimes they freeze momentarily in poised positions (potential), and sometimes they hold a stable form that endures (resonance). Throughout their routine, the overall “dance energy” doesn’t vanish or magically appear—it simply morphs between these states of motion, stability, or stored possibility.

When two dancers converge and whirl together, they accelerate, reflecting a rise in kinetic flow resonance. Later, they might separate and adopt a calm posture, shifting part of that energy into a potential-like stance. Yet the ballroom’s overall intensity—analogous to RLFlow’s total flow—remains balanced, as every move is just a rearrangement of how energy is shared among the dancers.

The Role of Resonance in Conservation

In RLFlow, resonance isn’t just about vibration; it underpins stability and synchronization across flows, shaping how energy is maintained throughout the flowfield. Here’s why resonance is crucial:

• Stability and Adaptation
  When two flows resonate, they sync up to form a stable pattern. That pattern may exhibit potential-like characteristics (stored energy) or kinetic aspects (continuous movement). If their resonance reconfigures, the type of energy shifts, yet the total intensity remains intact.
• Emergent Properties
  Both “mass” and “energy” emerge from resonant flows. Picture a whirlpool forming in a river: its apparent structure is maintained by flow resonance. The whirlpool’s energy comes from these interacting currents, and if outside conditions change, the whirlpool vanishes—but the overall flow intensity remains conserved in the system.

Resonance can be seen as the music guiding a dance—aligning the dancers (flows), allowing energy to shuffle among kinetic, potential, and resonance states without ever being lost. Through each transformation, the total energy in the flow continues onward, never ceasing, simply adopting new forms.

The RLFlow Conservation Principle vs. Classical Conservation

Classically, we treat conservation of energy as a bookkeeping task: energy moves from one type to another—say, kinetic to potential—like a currency that’s neither created nor destroyed. RLFlow offers a different perspective:

• Flow Redistribution
  Energy isn’t passed around as discrete blocks; rather, it adapts across resonating flows. The intensity is continuously redistributed, reflecting how these flows adjust to one another.
• Holistic Perspective
  Instead of focusing on individual objects, RLFlow frames conservation within the entire flowfield, from subatomic scales to cosmic expanses. It’s about an interconnected web of flows keeping the system in balance, rather than isolated particles transferring “energy units.”

By shifting from a mechanistic view of energy as “stuff” inside objects to a dynamic vision of intensities in a unified flow, RLFlow reimagines conservation as a process of ongoing equilibrium. The essence of energy never disappears; it simply changes shape to match the evolving resonance patterns of the flow.

Implications of Flow Intensity Conservation

1. A Unified View of Physical Forces

In RLFlow, forces such as gravity, electromagnetism, and even nuclear interactions emerge from resonant flows balancing and adjusting themselves:

• Gravitational Energy
  Traditionally, gravity is traced to mass or spacetime curvature. Under RLFlow, gravity emerges from intense flow resonances around massive bodies—what appears as “attraction” is really flows bending and redistributing intensity in a self-balancing pattern.
• Electromagnetic Energy
  Instead of discrete fields, RLFlow treats electromagnetic phenomena as dynamic resonances in the flow. The principle of energy conservation simply reflects how these resonant adjustments preserve total flow intensity, even as electric and magnetic configurations shift.

Seeing forces this way suggests all interactions are facets of one underlying flow equilibrium, making apparent differences in forces an outcome of how energy “settles” among resonance, kinetic, or potential modes.

2. Quantum Energy and Uncertainty

RLFlow also offers fresh insight into quantum behavior, often seen as random or paradoxical:

• Quantum Superposition
  RLFlow frames superposition as multiple resonance possibilities within a flow structure. The total flow intensity remains the same—distributed across potential states—until measurement “locks” the system into a single resonance pattern.
• Quantum Fluctuations
  The small oscillations we see in quantum fields can be viewed as localized variations in flow resonance. Even transient “virtual particles” fit the RLFlow picture if we interpret them as short-lived intensity redistributions that respect the overall conservation of the flowfield.

By focusing on resonance and stability, RLFlow provides a more deterministic mechanism behind quantum randomness: energy never disappears; it merely flows among overlapping resonant states.

3. Energy and Cosmic Evolution

On the cosmic scale, flow intensity conservation casts new light on major astronomical puzzles:

• Expansion of the Universe
  In standard cosmology, dark energy drives universal expansion. RLFlow reimagines this process as an expanding flowfield redistributing its resonance intensity over larger spaces. The “push” we label as dark energy could simply be flows diverging, yet maintaining total intensity overall.
• Black Holes and Conservation
  Where general relativity sees infinite density, RLFlow sees maximal resonance. Matter and energy drawn into black holes become part of a hyper-concentrated flow. Energy remains conserved, compressed into a peak resonance state rather than vanishing. Even Hawking radiation can be interpreted as minor resonant fluctuations at the black hole boundary, letting some energy flow back out.

From galaxy formation to the life cycle of stars, RLFlow implies these cosmic happenings are driven by the same principle: total flow intensity remains constant, no matter how drastically the universe’s energy distribution shifts.

By centering on continuous flow instead of discrete states, RLFlow merges quantum nuances, celestial mechanics, and everyday physics into a single fabric—one that highlights how energy’s form can change, but its essence remains conserved across all scales.

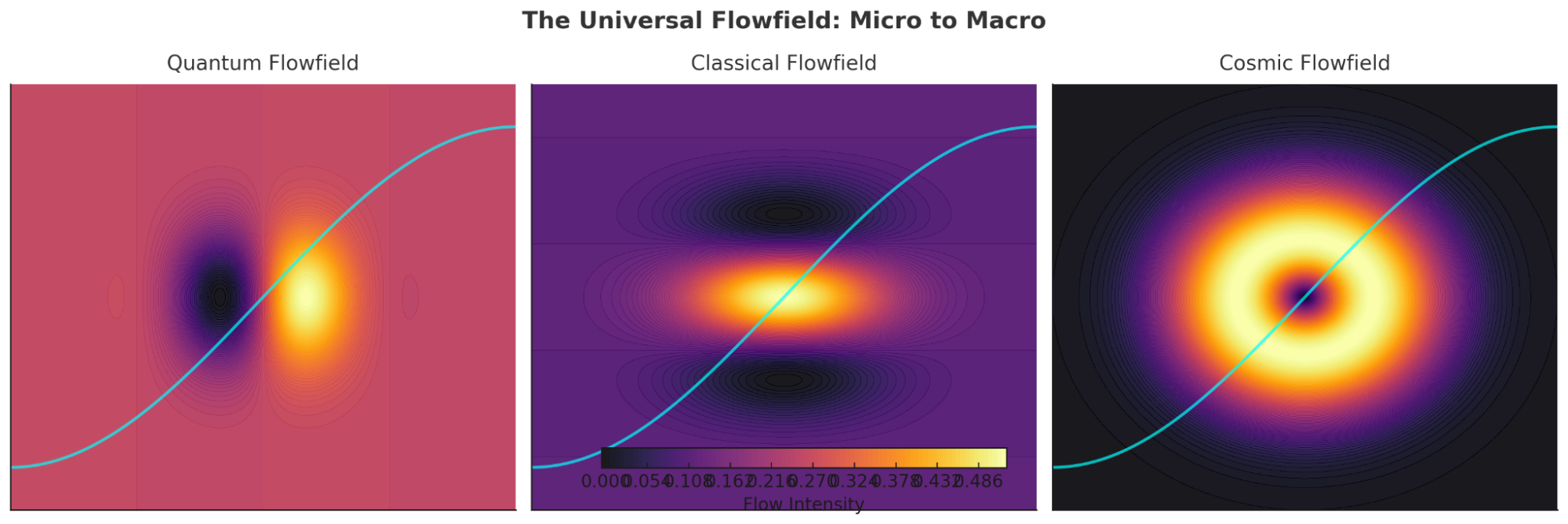
"The Universal Flowfield: Micro to Macro," illustrating RLFlow’s conservation principle across different scales. The three panels depict:

1. Quantum Flowfield – Resonating wave patterns representing subatomic flows.
2. Classical Flowfield – Fluid-like or electromagnetic interactions at a macroscopic scale.
3. Cosmic Flowfield – Galactic structures and cosmic flows showing large-scale energy conservation.

A New Paradigm for Understanding Energy

The RLFlow framework brings energy, forces, particles, and cosmic phenomena together under one unifying principle: Conservation of Flow Intensity. Here’s a concise summary:

• Flow Intensity Conservation
  Rather than energy being “carried” by discrete particles, RLFlow sees it as the inherent resonance within interacting flows. The total intensity remains constant, even as it changes expression.
• A Single Fabric for All Energies
  Kinetic, potential, gravitational, electromagnetic—each is just a different mode of these underlying flows. By focusing on flow dynamics, RLFlow unifies what classical physics often treats as separate energy categories.
• Quantum Scale, No Paradoxes
  At the quantum level, oscillatory flows preserve energy across “superposed” states, making phenomena like wavefunction collapse more intuitive. Instead of paradoxes, RLFlow’s flow resonance provides a deterministic mechanism for how energy is conserved in probabilistic events.
• Cosmic Reach
  From the universe’s expansion to the ultra-dense resonance of black holes, flow intensity conservation offers a broader, more interconnected view. It shows how large-scale structures retain energy balance across vast stretches of space and extreme conditions.

In essence, RLFlow redefines energy as a dynamic, shared property of the cosmos—constantly adapting yet never vanishing. Instead of picturing energy as a commodity in isolated systems, we now see a continuous fabric of flow, resonating throughout reality and weaving everything together.

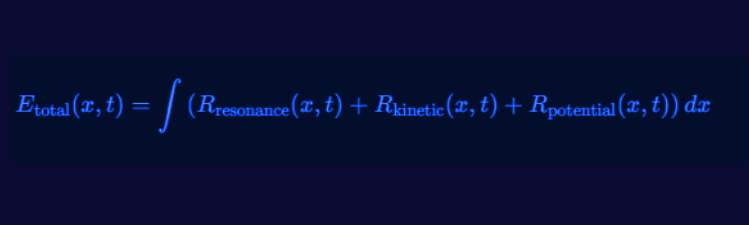
Breakdown of Each Component

1. E_total(x, t): Total Energy in the Flowfield

Definition: Represents the complete energy of a system at any given point in the flowfield, combining resonance, kinetic, and potential energy components.
Significance: Unlike classical physics, where energy is seen as discrete packets tied to objects, E_total describes a holistic view where energy is an intrinsic property of the interconnected flowfield.

2. R_resonance(x, t): Resonance Energy

Definition: The baseline, rest-like energy that arises from stable flow patterns. It reflects the stability of flows and their capacity to persist over time.
Law Connection: Related to the First RLFlow Law—Flow Stability (Flow Inertia). Resonance energy embodies the stability and intrinsic persistence of flows, much like inertia in classical physics.
Metaphor: Imagine a calm whirlpool in a river. Its steady rotation represents resonance energy—a stable pattern requiring no external input to persist.

3. R_kinetic(x, t): Kinetic Energy

Definition: Energy associated with the motion of flows. It depends on the velocity and intensity of the flowing system, reflecting how energy moves dynamically within the flowfield.
Law Connection: Related to the Second RLFlow Law—Flow Interaction. Kinetic energy emerges from the dynamic redistribution of flow energy during interactions.
Metaphor: A rushing river represents kinetic energy—motion-driven energy that transforms as flows accelerate or slow down.

4. R_potential(x, t): Potential Energy

Definition: The stored energy within a flow configuration, representing the capacity for future changes. It’s the buildup of energy within a specific arrangement of flows.
Law Connection: Related to the Third RLFlow Law—Reciprocal Flow. Potential energy emerges from flow arrangements poised to shift into motion or new configurations.
Metaphor: Water held behind a dam exemplifies potential energy—an arrangement waiting to release motion.

5. ∫ dx: Integration Across the Flowfield

Definition: The integral sums up the contributions of resonance, kinetic, and potential energy over the entire flowfield, capturing the total energy within a system.
Significance: By integrating over space (x), this approach acknowledges the interconnected nature of the flowfield, where energy forms are distributed and continuously interact.

Key Insights from the Equation

Conservation of Flow Intensity

The total energy E_total(x, t) is always conserved. While the forms of energy—resonance, kinetic, and potential—can transform into one another, the total flow intensity remains constant.

Dynamic Transformations

Energy transitions between forms, but the sum of all energy types in the system never wavers:

• Resonance → Kinetic: Stability becomes motion.
• Kinetic → Potential: Motion rearranges into stored energy.
• Potential → Resonance: Stored capacity stabilizes into a persistent pattern.

Unified View of Energy

RLFlow combines classical principles (e.g., conservation of energy) with a more fluid, interconnected understanding. It shows that energy is not static but dynamically evolves with the flowfield.