Flow Dynamics – Chapter 2

Explore the redefinition of Newton’s Laws of Motion in the RLFlow Model.

Redefining Newton's Laws of Motion

Imagine if Isaac Newton were here today, learning that his foundational laws of motion—laws that have been guiding science for centuries—could be reimagined from an entirely new perspective. Instead of being static, fundamental truths, what if mass and force were dynamic properties, emerging from deeper, more interconnected processes?

In the RLFlow model, mass is not an intrinsic property of an object. Instead, it arises from the density of flows—patterns of movement within a larger cosmic flowfield. Likewise, force is no longer a simple push or pull, but an interaction between dynamic flows, twisting and weaving through the universe. This is not about discarding Newton’s ideas, but about expanding them—seeing them through the lens of a more interconnected, flowing reality, perhaps even one that feels more alive.

The RLFlow model challenges us to translate Newton’s timeless principles into the language of flows, where the concepts of motion, mass, and force take on new meanings. Let’s start by breaking down each of Newton’s laws and understanding how they transform in this flow-based framework.

First Law Reimagined: Law of Flow Stability

Newton's First Law states that an object at rest stays at rest, and an object in motion stays in motion unless acted upon by an external force. In RLFlow, this principle remains recognizable, but it takes on a new form. Here, inertia is seen as the tendency of a stable flow pattern to maintain its structure. When there is no external disturbance, the flow continues in its original form—whether it’s stationary or moving steadily.

In other words, a flow remains stable unless something from outside interacts with it. The resonance factor, denoted as R(x,t), describes the stability and persistence of the flow. When there is no external flow interaction, the resonance remains unchanged, and the flow stays as it is—no force, no acceleration.

First Law: Law of Flow Stability (Flow Inertia)

Stable flows persist unless disturbed. Inertia is not just about an object’s resistance to change, but the persistence of a stable flow pattern in the absence of external influence.

Mathematical Representation:

Where:

• R₁(x, t) represents the resonance of the initial flow.
• R₂(x, t) represents potential external disturbances (other flows).

In simple terms, inertia here is just the persistence of a stable flow—like a river that flows steadily until something changes its course.

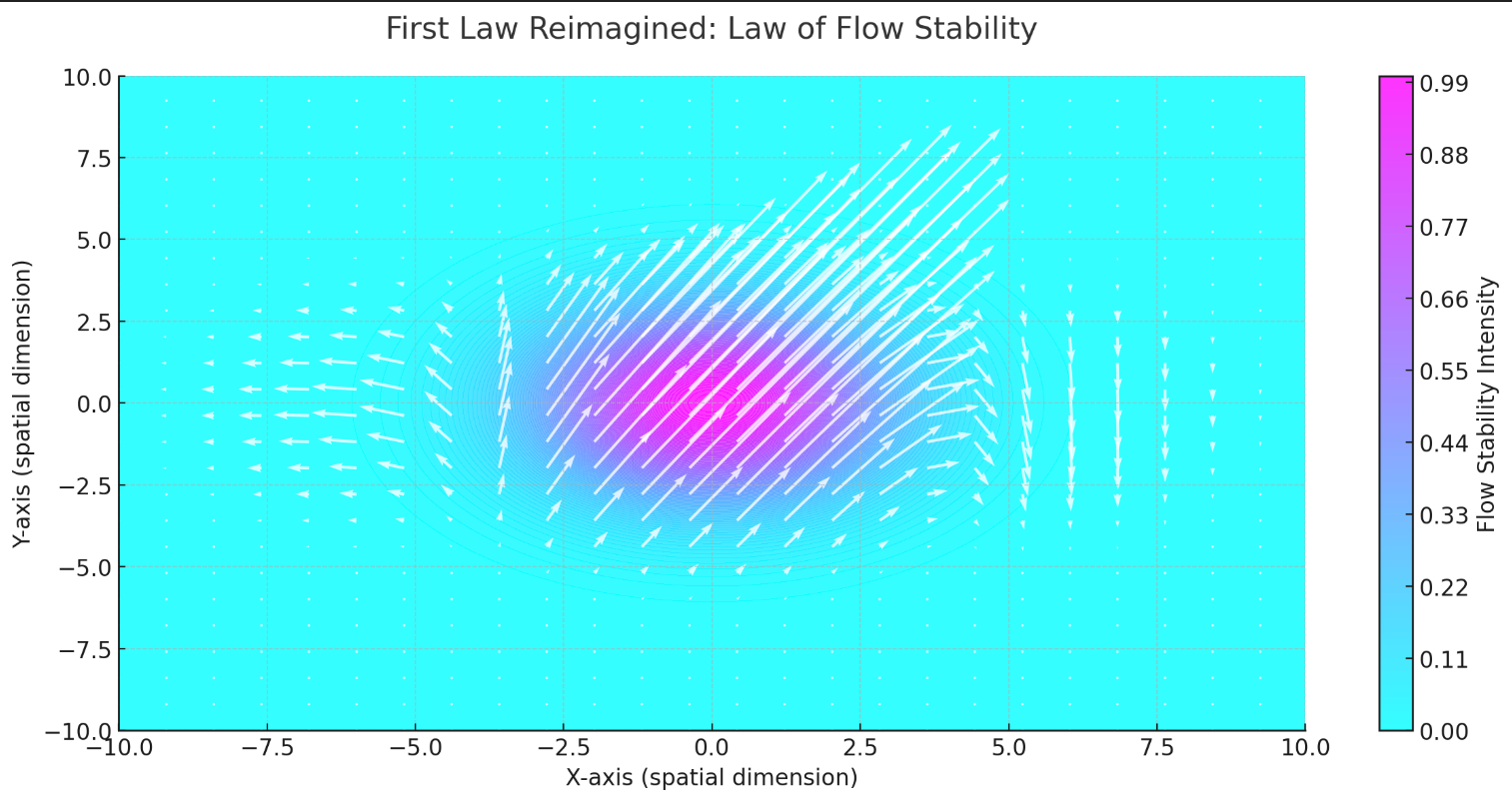
This visualization represents the First Law Reimagined: Law of Flow Stability. The color map illustrates the stable flowfield, while the vectors depict the effects of external disturbances. Without disturbances, the flow remains stable, embodying the RLFlow principle of persistence unless acted upon by external influences.

Metaphor: Imagine a river flowing calmly along its path. In places where it’s smooth and steady, the current maintains its shape and direction—everything moves predictably. Now, think of a small, still pool just off the river. This pool is calm and undisturbed, content to stay that way. Unless an external force, like a stone or wind, disrupts it, the water remains tranquil. This is how inertia works in the RLFlow model—the still pool represents a flowfield in balance, maintaining its form unless acted upon by an outside disturbance.

In the RLFlow model, inertia is like that calm pool of water—stable and steady until something from the outside comes along and changes it. It is the natural stability of flows, reflecting Newton’s idea that things in motion stay in motion unless influenced by something else.

Second Law Reimagined: Law of Flow Interaction

Newton's Second Law tells us that force equals mass times acceleration (F=ma). This equation explains how an object’s mass and the force acting upon it determine its acceleration. But what if mass isn’t a fundamental quantity, but an emergent property of the flow itself? In the RLFlow model, mass is simply the density or stability of a particular flow pattern. This changes everything.

Instead of force being an external push or pull on a solid object, force in RLFlow is the interaction between flows, and acceleration is the result of these flows dynamically influencing each other. The more intense the interaction, the greater the effect—the greater the "force." Mass, in this sense, becomes the density of the flow, describing how much resonance or concentration a particular flow pattern possesses.

The redefined Second Law in RLFlow becomes:

Second Law: Law of Flow Interaction (Flow Interaction)

Force arises from the interaction between flows, with changes in flow resonance being akin to acceleration. Mass is no longer a fixed quantity but emerges from the flow's density and stability.

Mathematical Representation:

Where:

• R₁(x, t) represents the resonance factor of the first flow.
• (∂/∂t)R₂(x, t) represents the change in the flow resonance over time, analogous to acceleration.

In this formulation, force is described as the interaction between two flows, where one flow changes over time. This change is like acceleration, but instead of being related to a traditional mass, it’s related to the intensity and stability of the flow pattern.

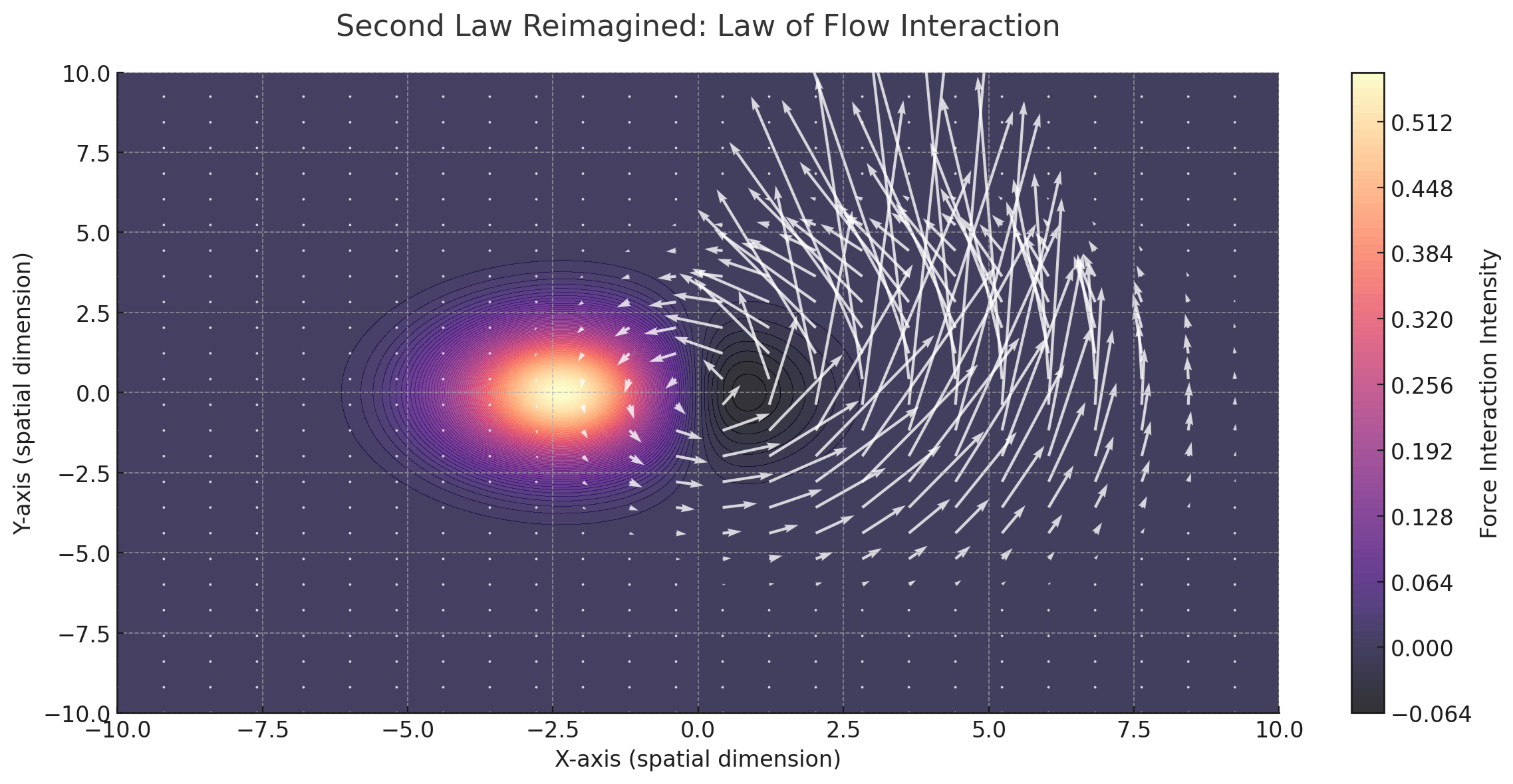
This visualization represents the Second Law Reimagined: Law of Flow Interaction. The color map shows the intensity of the force arising from the interaction between two flows, while the overlaid vectors illustrate the changes in resonance and their dynamic interplay.

Imagine a stable whirlpool in a calm section of a stream (R1). Now picture a sudden surge of faster-moving water entering from upstream (the changing R2). As this faster current arrives, it stirs the whirlpool, making it spin faster or change shape. The “force” you see is really just the whirlpool responding to this new, changing current. The more drastic the change in the incoming flow, the bigger the resulting effect on the whirlpool’s intensity.

Metaphor: Picture a whirlpool in a stream. The whirlpool spins steadily, pulling water into its center. Now imagine the current in the stream begins to speed up—the whirlpool responds by spinning faster, drawing in more water and energy. The rate at which the whirlpool's speed changes is the equivalent of acceleration. The interaction between the faster-flowing current and the whirlpool creates a stronger, more intense force.

In the RLFlow model, mass is the density and stability of the whirlpool—essentially, how tightly the flow is concentrated and maintained. The more stable and dense the whirlpool, the more energy it takes to change its flow. Force, therefore, is like the effect of the increased current on the whirlpool—the stronger the interaction, the greater the resulting change in the flow’s intensity.

So, in RLFlow:

• Mass is no longer a static property but a measure of flow density.
• Force is the outcome of flows dynamically interacting with each other.
• Acceleration is the change in the flow resonance over time.

Think of it as an interplay between different currents in a river. The greater the difference in intensity and direction of the flows, the greater the impact each flow has on the other—creating what we perceive as force.

Summary of the Second Law: In traditional physics, Newton's Second Law connects force, mass, and acceleration. In RLFlow, force arises from the interaction of flows, where the change in resonance represents acceleration. Mass is not an inherent property of a body but emerges from the flow's density and stability. The Second Law now reflects the dynamic interactions of flows, making it applicable not just to macroscopic motion but also to quantum phenomena and cosmic scales.

Third Law Reimagined: Law of Reciprocal Flow

Newton’s Third Law tells us that for every action, there is an equal and opposite reaction. In simple terms, if one object exerts a force on another, the second object exerts an equal and opposite force back. This law has always reflected the natural balance of interactions in our universe, and in RLFlow, it continues to do so—but in the context of flows.

In the RLFlow model, action and reaction are viewed as reciprocal interactions between flows. When two flows meet, they influence each other equally—bending, twisting, or resonating in opposite directions. These interactions are dynamic and continuous, and each flow affects the other in a perfectly balanced manner.

The redefined Third Law in RLFlow becomes:

Third Law: Law of Reciprocal Flow (Flow Reciprocity)

For every action, there is an equal and opposite flow interaction. Forces are not merely between static objects but are the result of flows resonating and adjusting to one another in balanced, reciprocal relationships.

Mathematical Representation:

Where:

• R₁(x, t) and R₂(x, t) are the resonance factors of the interacting flows.

In this formulation, the force exerted by one flow on another is mirrored by an equal and opposite reaction from the second flow. Instead of viewing these as separate forces acting on different objects, RLFlow considers them as dynamic exchanges of resonance—ongoing interactions that maintain balance within the flowfield.

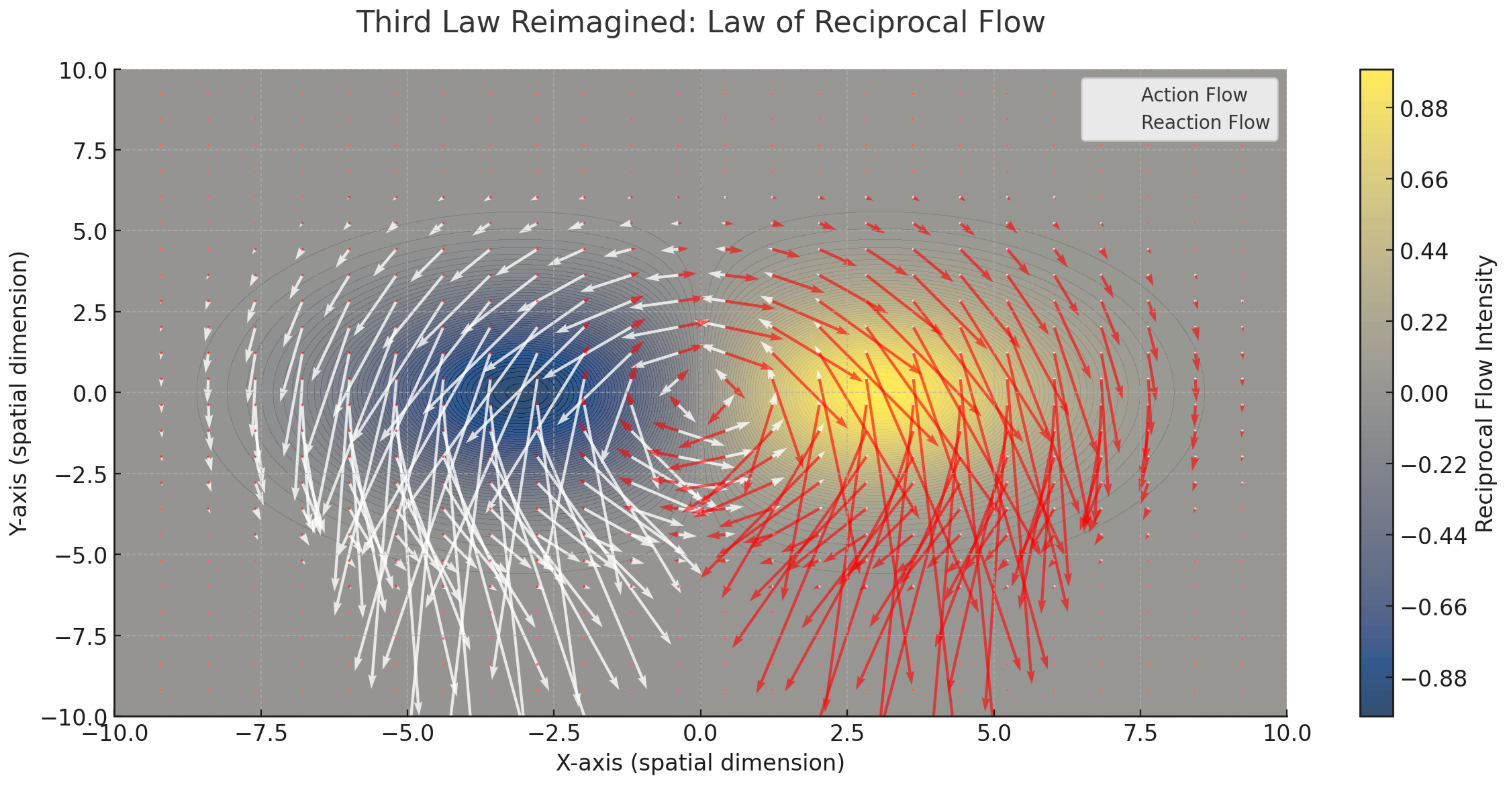
This visualization represents the Third Law Reimagined: Law of Reciprocal Flow. The color map depicts the combined intensity of reciprocal flows, while the overlaid vectors highlight the equal and opposite interactions between the flows.

Imagine two people in a small boat: When one person shifts their weight, the boat tilts. Instantly, the other person feels this tilt and naturally adjusts their own position to keep the boat balanced. The result is a set of equal and opposite adjustments—one person’s movement (the action) is balanced by the other’s movement (the reaction). They’re not solid objects pushing each other in a vacuum, but two people balancing each other’s shifts in a continuous, fluid interaction.

Metaphor: Imagine two waves in the ocean approaching each other. As the first wave moves forward and rises, the second wave dips in response. But the second wave doesn’t simply absorb the impact; it pushes back with an equal force, creating a dance of rising and falling that keeps both waves in motion. This rhythmic exchange of forces is what we traditionally understand as action and reaction.

In the RLFlow model, the interaction between these two waves is not about separate entities pushing and pulling each other; it is about how flows adjust to maintain equilibrium. When two flows meet, they create patterns of resonance, where each flow mirrors the influence of the other. It’s a harmonious exchange, like two dancers moving in sync, each anticipating and balancing the movement of the other.

Summary of the Third Law: Newton’s Third Law states that for every action, there is an equal and opposite reaction. In RLFlow, this becomes the Law of Reciprocal Flow, describing how flows dynamically interact to maintain balance. Forces are not static pushes or pulls but continuous, adaptive exchanges of energy within the flowfield. The interaction of flows creates resonance, where every action is met with an equal, reciprocal adjustment, maintaining the harmony of the flow.

Summarizing the RLFlow-Based Laws:

1. First Law (Flow Inertia):
   • Flows maintain their structure unless disturbed. Inertia is the persistence of a stable flow pattern, emphasizing the natural stability of flows in the absence of external influence.



2. Second Law (Flow Interaction):
   • Force is the interaction between two flow structures, where the change in flow resonance over time corresponds to acceleration. Mass is an emergent property of the flow's density and stability.



Every small region’s contribution adds up, showing how the overall flowfield responds to changes, creating force as a result of evolving patterns, not just rigid objects.

3. Third Law (Flow Reciprocity):
   • For every action, there is an equal and opposite flow interaction. Forces arise from reciprocal flow adjustments, creating a balanced, dynamic exchange of resonance.



This shows that the interaction is always balanced: any action by one flow is naturally met by an equal and opposite response from the other flow.

Closing Thoughts

By reimagining Newton’s laws through the lens of RLFlow, we are not discarding the old framework but rather expanding it to encompass a more interconnected and dynamic reality. In the RLFlow model, mass, force, and motion are not static properties but emergent behaviors of flows interacting in a cosmic dance.

This new perspective doesn’t just help us understand Newton’s principles on a deeper level—it opens up new realms of possibility. We can now explore phenomena at the quantum level, where uncertainty and superposition can be explained through flow dynamics, or at cosmic scales, where the behavior of galaxies and gravitational waves can be understood as resonances within the flowfield.

Newton’s contributions laid the foundation for our understanding of motion. Now, with RLFlow, we move beyond rigid definitions to see the universe as it truly is: a flowing, dynamic system, where every part influences the others in a continuous dance of balance and resonance.